a)Quais são as raízes da função? b) A função admite um valor máximo ou mínimo? Que valor é esse?
c) Determine o conjunto-imagem da função.
Anexos:
Soluções para a tarefa
Respondido por
1
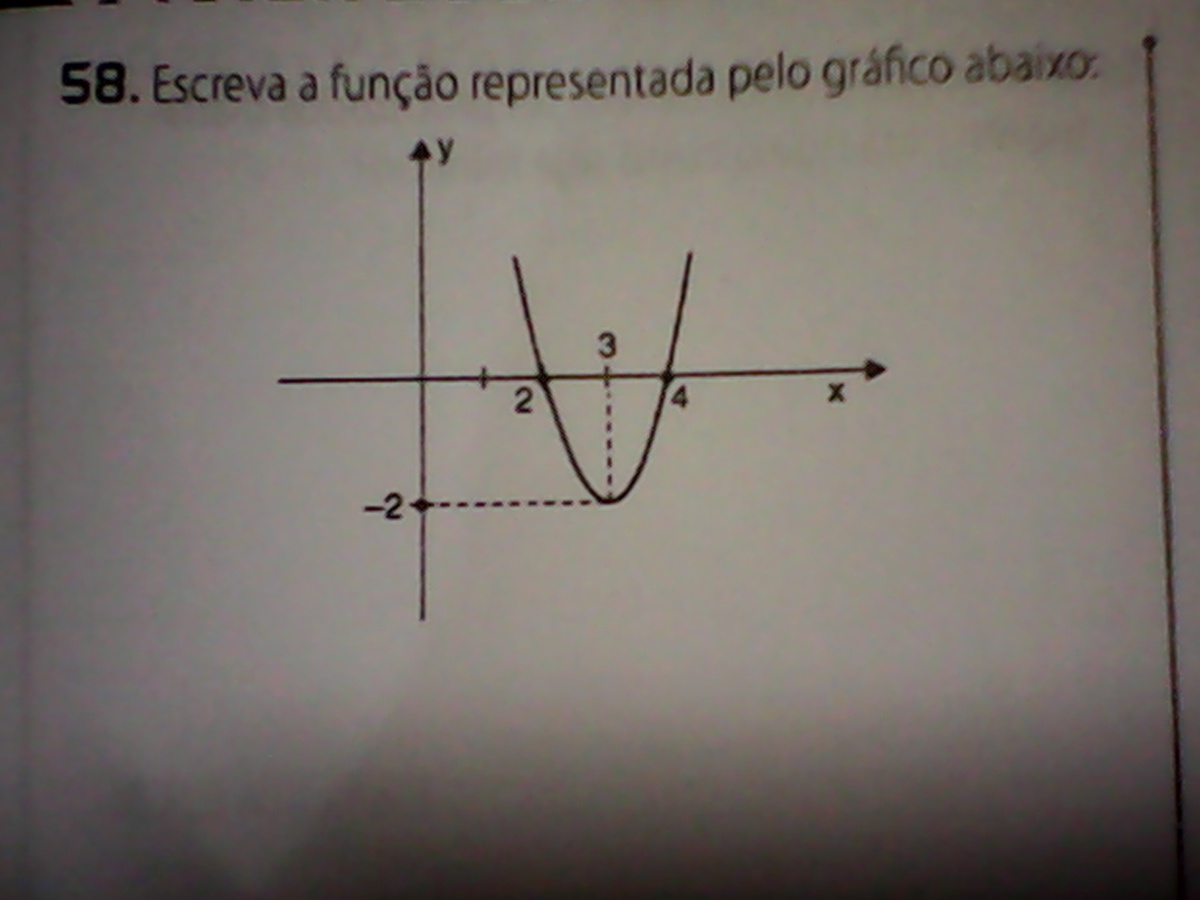
as raízes da função são quando y=0 , basta olhas os pontos de x onde y=0 , podemos ver que são quando x=2 e quando x=4
a função admite valor mínimo pq sua concavidade é voltada pra cima
logo o ponto mínimo = (3,-2)
o conjunto imagem é y> ou igual a -2
a função admite valor mínimo pq sua concavidade é voltada pra cima
logo o ponto mínimo = (3,-2)
o conjunto imagem é y> ou igual a -2
geiselucid:
Oi Ronaldopavione ,qual seria a função representada por esse gráfico??Pode me ajudar?Obrigada!
essa função é uma função quadrática, ou função do segundo grau, a forma dela é uma parábola
É que no exercício pede para representar a função através do gráfico...
Respondido por
1
Raízes da função: onde corta o eixo x. 2 e 4.
Função admite valor mínimo, pois a concavidade do gráfico é para cima. Valor mínimo da função=valor mínimo de y= -2
Imagem da função é todos os valores que y pode assumir. Nesse caso, de -2 até mais infinito, pois você pode prolongar as pontas dela até o infinito e como possui mínimo (-2) e não máximo, o infinito é positivo.
Função admite valor mínimo, pois a concavidade do gráfico é para cima. Valor mínimo da função=valor mínimo de y= -2
Imagem da função é todos os valores que y pode assumir. Nesse caso, de -2 até mais infinito, pois você pode prolongar as pontas dela até o infinito e como possui mínimo (-2) e não máximo, o infinito é positivo.
Perguntas interessantes