Question

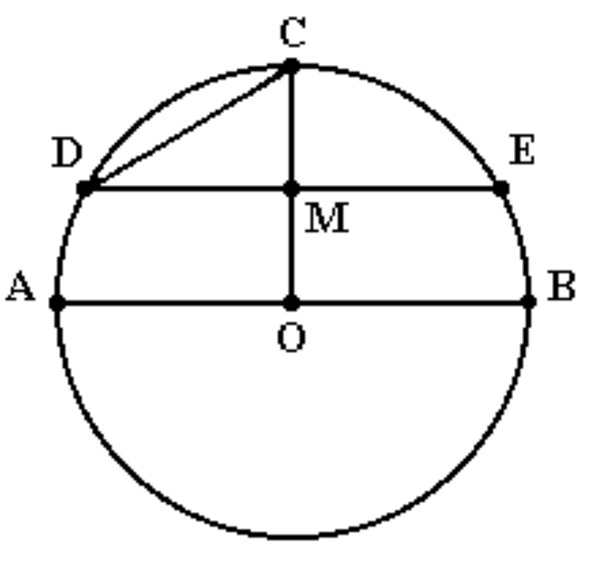
Nessa figura, (ver anexo) o segmento AB é diâmetro da circunferência de centro O e raio 12, o segmento OC é perpendicular ao segmento AB, e o segmento DE é paralelo ao segmento AB e M é ponto médio do segmento OC.  A medida DC é:

a) 8
b) 9
c) 10
d) 11
e) 12

O gabarito é 12 letra (E), mas como chegar nisso?

agradeço

Answer 1

Veja a imagem que anexei. Apenas tracei o raio OD e coloquei umas medidas

Sendo M o ponto médio do segmento OC, os segmentos OM e MC são iguais, e medem a metade de OC. OC é o raio da circunferência, que mede 12, logo OC e MC medem 6.
____________________

Aplicando o teorema de pitágoras no triângulo ODM:

$r^{2}=x^{2}+(r/2)^{2}\\12^{2}=x^{2}+6^{2}\\144=x^{2}+36\\144-36=x^{2}\\x^{2}=108$

Agora, vamos aplicar o teorema de pitágoras no triângulo DCM:

$(\overline{DC})^{2}=x^{2}+(r/2)^{2}\\(\overline{DC})^{2}=108+6^{2}\\(\overline{DC})^{2}=108+36\\(\overline{DC})^{2}=144\\\overline{DC}=\sqrt{144}\\\overline{DC}=12$

Letra E